Map Borders (Part 11)

I have two major items left on my initial map borders list: Celtic knots and corner boxes.  In this post I start working on Celtic knots.  Although they look simple, it was not intuitive to me how to construct and draw them, so this installment proceeds fairly slowly to describe Celtic knots and illustrate how they “work." 

For those of you who are unfamiliar with Celtic knots (or unfamiliar with the term), Celtic knots are a kind of illustrated braidwork that has been used as a decoration for many years, including on medieval manuscripts.  Here's a simple example:

The interlacing of the various strands is the defining characteristic of Celtic knots.  Among their uses, they've long been popular as an element in map borders.  Here's an example from one of my inspirational maps:

Here's another one, with a more complicated pattern:
The key feature of Celtic knotwork is that each cord crosses other cords in an alternating pattern: first over, then under, then over, and so on.  If you trace any cord in the example above you'll see that's true.

What was not so obvious to me initially is that a row of crossings always have the same “handedness".  That is, every crossing in the top row of this braid has the same cord on top:

And then the next row of crossings has the other handedness, to maintain the over/under pattern:

So you can immediately tell how two cords should cross by the row they appear in.  (Or to put it another way, you can draw all the crossing in a row the same way.)

Another feature of knots is that the crossings alternate columns:

The crossings in all the red columns have the same handedness and the crossings in all the blue columns have the other handness.  (Another way to put this is that the rows are offset from each other.)

Now take another look at the example knot:

Notice anything about it?  It was drawn incorrectly!

In the bottom row, the cords go over-over (and under-under) instead of over-under as they should.

(Ironically, the first Celtic knot from my inspirational maps is not a true Celtic knot either; it has three rows and Celtic knots always have an even number of rows.)

With some insight into the crossings, let's look at the edges.  When a knot is artistically drawn it may not be immediately apparent, but at the edges of the design the cords “bounce off" of invisible walls at 90 degree angles:

Here you can see how the blue cord hits the top edge of the pattern and “bounces off."  In the corners, the cord bounces twice.  Knotwork is usually drawn with the cords following the walls (as in this example) or with rounded turns (as in the broken knotwork example above) which somewhat obscures the way the cord bounces off the edges.

That's about all you need to know to understand a simple braid.  What about a more complex pattern?

More complex patterns are created by adding additional walls where the pattern is interrupted and reflects off the new walls just as it does with the edges.  In this case, I've added three walls:

In the bottom corners, the pattern now bounces off three walls in row.

The last thing you might want to note is that spaces between the crossings form a regular grid, and the walls always connect two dots on this grid:

The crossings (or reflections of walls) all happen halfway between the red dots.  Here's a picture of the above pattern showing just the walls and the grid:

The big black dots here correspond to the red dots above, and the gray dots are the in-between dots where the cords cross or reflect off of walls.  This diagram also suggests a representation / implementation for Celtic knots:  an array where the black dot positions are ignored, and the gray dot positions are either “open," “vertical wall," or “horizontal wall."  Patterns can be created by placing a few walls into the array and leaving most positions “open."

The illustration above comes from a very useful online Celtic knot tool that you can find here.  That will let you play around with placing walls and designing patterns.  Try it out, it's quite entertaining!  For more interesting information on Celtic knotwork, see the tutorial here.  The tutorial has a clear explanation of how knotwork is designed and drawn.  The tutorial here provides an alternate explanation in terms of graph theory.

Now that I have an understanding of Celtic knotwork and an idea of how to represent a knot, let me  consider how to draw a knot from the representation.

My initial thought was to draw the knot as a series of paths, each one tracing completely through one of the loops of the knot.  I could start at one of the gray dots and trace through until I returned to the same dot, creating the path to draw.  However, I realized pretty quickly that this wouldn't work.  The problem occurs in the crossings.  In each crossing, I need one path to be atop the other path.  I thought I could do this by masking out the lower path.  (A mask blocks an area of the image from showing, so by blocking whichever path was supposed to be on the bottom, the other path would appear like it was on top.)  But many times a path crosses itself.  In that case, masking out the bottom path would also mask out the top path!

So I will have to draw the paths piecemeal.  I can certainly draw a whole path from one crossing to the next crossing, but since I'm drawing piecemeal anyway, it seems worthwhile to think about the smallest pieces I can draw.

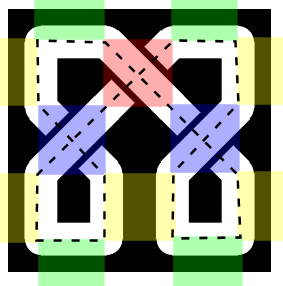
As it turns out, you can draw any Celtic knot using just four pieces:  a left-handed crossing, a right-handed crossing, a two-sided vertical wall reflection and a two sided horizontal wall reflection:

(If you allow rotations, this is only two pieces, but for illustration purposes I am using four.)  There are two tricks to keep in mind.  First, at the edges of the knot you use only half of the reflection patterns.  Second, where two reflections meet (as in a corner) it is usually drawn more smoothly than just sticking two reflections together.

Here's a simple example of a knot:

And here's the same knot with the different pieces identified:

Note that there are holes between each of the pieces, corresponding to the big black dots in the diagram above.  Nothing needs to be drawn in these areas.  This is clearer if the path is drawn as a thin line:

You can see that in the red and blue tiles, you draw two lines crossing the tile; in the yellow and green tiles you draw two lines along the edges of the tiles.  If you make the lines connect properly at the edges of the tiles, you get a Celtic knot.

To review:  Celtic knots are composed of cords that follow an over/under pattern of crossing and reflect off the edges of the pattern and off of internal walls.  A knot can be represented as an array of points.  Points represent crossings or vertical or horizontal walls.  All crossings in the same row of array cross the same way, and alternating rows have alternating crossings.  To draw a knot from an array, you draw in each point the appropriate crossing or wall, and connect each point to it's neighboring points.

Next time I'll get started on implementing a representation and displaying it.