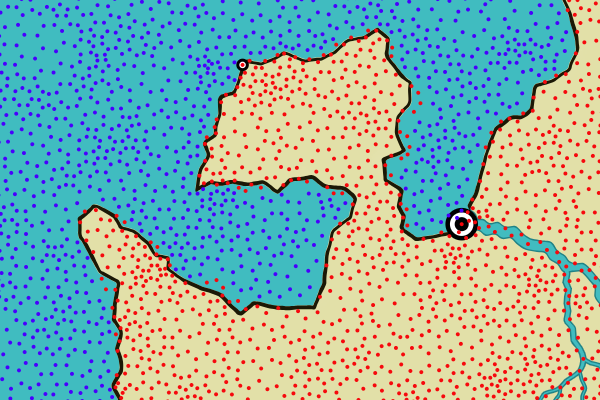
This was pretty unsatisfying -- both because the island was very jagged and because the size of the details was too big. Greatly increasing the number of Delauney triangles (and hence making each triangle much smaller) would seem to address this problem -- but at the density of triangles I would require the browser crashes.
I addressed this by divorcing the land outlines from the underlying location representation. This allowed me to draw islands any shape or size I wanted, regardless of the underlying grid of locations:
So, problem solved! This allows me to draw barrier islands, and since the coastline no longer has to follow the underlying grid, if I want a more detailed coastline I can create a coastline as normal and then add detail to it.
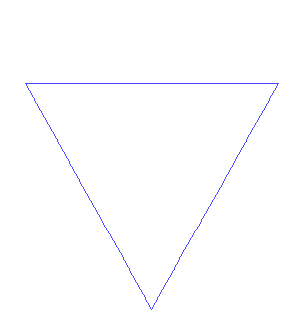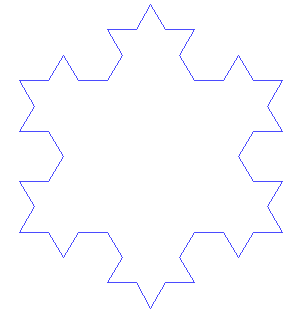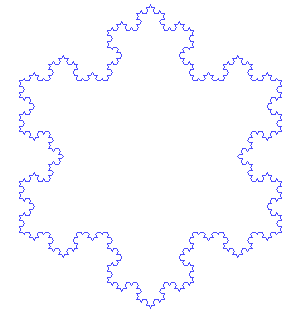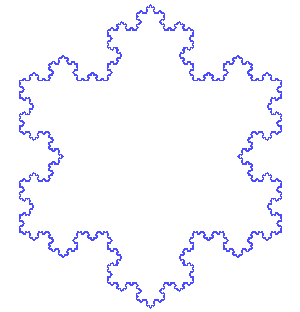
Except... How do you add detail to a coastline? That isn't as easy as you might think. Since I want a fractal coastline, I looked at using actual fractals to add detail to the coastline:
with a broken shoreline, a variety of different shaped islands, etc.
Perlin noise can produce this sort of terrain with a sufficiently detailed underlying grid, but can it be done *without* storing the terrain height values in an underlying grid with the required resolution (since I know that breaks my code)? So far, I haven't figured out how to do that. The coastline is essentially the path through all the points where the Perlin noise function has a value of zero. Although you can find out directly from the Perlin noise function a value at a particular (X,Y) location, you cannot find (say) “all the locations where the function has a value of zero." So it's difficult to see how you can trace out the height contour without an underlying grid.
Even worse, I asked Amit how to do this, and he didn't have an answer either. It's one thing when I can't figure it out, but when the smart guy can't figure it out I begin to think it can't be done. Frustrating. I have the capability to shape the coastline however I want, but I can't get the shapes I want without a very detailed underlying grid.
So how can I get a high-resolution grid without breaking my code?
One approach I've thought about is something Azgaar did in his map generator -- variable size Voronoi cells. The basic idea is to increase the density (and reduce the size) of the underlying grid along the coastlines, and make it less dense in the oceans and other areas that do not need the detail. With this option, you will have many grid cells only in the areas where you need the detail. This would be a pretty challenging change to implement in Dragons Abound, but it's something I want to think about. On the other hand, Azgaar himself wasn't too happy with this approach, so that's also something to keep in mind.
In the meantime, I want to investigate exactly what is causing the browser to crash when I had lots and lots of triangles. The Chrome developer tools can provide a lot of insight into performance. I'm by no means an expert in how to use the tools, but many of the features are simple enough for anyone to figure out. Case in point, if you want to know the overall memory use in a program, the Memory tab shows the current usage:
In this case, I'm displaying Azgaar's web page and it is using a modest 20 MB of memory. I can use this to give me some basic insight into the memory usage of Dragons Abound and determine the point at which I crash the tab.
The basic parameter that controls the resolution of the underlying grid in Dragons Abound is cleverly called “npts" for Number of Points. For every unit area of the map (the regional maps I normally use as examples are 1 unit in area), Dragons Abound creates this many locations in the underlying grid. Typically I use a value of 16K (16384) for npts, which roughly means that each location in the grid corresponds to about a 70 square pixels on the screen at the default magnification.
Exact memory usage will obviously vary from map to map, but for the above map with 16K points, the memory usage was about 92 MB:
Which was lower than I expected and overall seems pretty modest.
If I double the number of points in the underlying grid, the memory usage goes up to 138 MB:
The memory usage doesn't double because some of that memory is overhead and other data structures that didn't change in size. The 16K additional points amount to about 50 MB of memory, so each point ends up using about 3K bytes of memory. That's more than I expected, but the overall usage is still very modest. On a computer with 64GB of memory, 150 MB is hardly noticeable.
Skipping ahead a few doublings, I find that the tab that Dragons Abound is running in usually crashes around 128K points. If I catch it before it crashes and check the memory:
which is ... not much. Certainly not enough to crash the tab.
I've been operating under the assumption that memory usage was crashing the tab, but apparently memory is not the problem. So why is the tab crashing on me? The only other clue I have is that the tab doesn't crash until the map is complete, so perhaps that's an indication that it is crashing during rendering.
The obvious guess is that the SVG I'm producing is overwhelming the browser renderer, either because it is too big or too complex. As a first step, I can investigate how many SVG elements I'm creating. In D3, I can get the total number of SVG elements I've created with svg.selectAll('*').size().
Running with 16K points and checking the number of SVG elements shows me this:
In turn, 32K points has 65457 elements and 128K points has 258823. Each point added to the underlying grid adds two elements to the map. I think I've found my culprit.
Each point in the underlying grid adds SVG elements because of the way Dragons Abound renders the land (and the sea). The land is rendered by drawing each underlying location as a filled polygon and then blurring them all together. This enables Dragons Abound to mottle the land in pleasing ways, or use the height of the land to render the land in 3D shading, as you can see in the land here:
I can investigate by turning off the land and ocean visualizations and checking to see how many SVG elements are created. With 256K points:
Wow, that's a huge reduction in the number of SVG elements. And as hoped, the map now renders without crashing! So as long as I avoid using the grid to render the land and sea, I can use a much denser grid than I've ever been able to before.
Now that I can use a much denser Voronoi grid, I want to check to see whether that enables generation of the sort of land features I want, such as coastal islands. The dense Voronoi grid creates other problems (especially with rivers) so I'll turn off everything except the coastlines to speed up testing and focus on that. Here's an initial render of some coastline using 256K points and some default noise:
The good news is that this renders fine, and in fact already produces a much better coastline.
Even without tuning it's a big improvement. The noise is producing the kinds of fractal coastlines and coastal islands that I noted above in the reference map.
Here's a 300% zoom on the islands:
At this magnification, you can see some of the triangle artifacts from the underlying grid, but even so the islands are able to form some interesting shapes. I can use smoothing (as I do on the current maps) to remove some of the more obvious triangle artifacts. At the default magnification this provides a less jagged coastline, but also removes some fine detail:
I'll probably have to tune that to find a good middle ground. More on that next time!