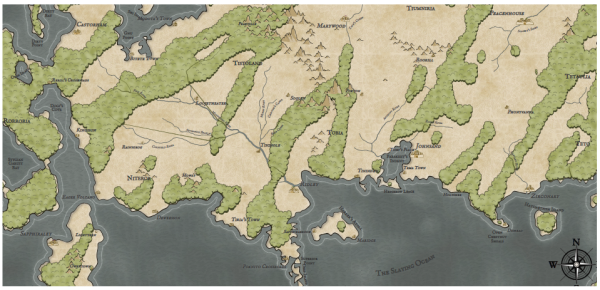
One thing you might notice about this map is that all the forests run generally southwest-northeast. That's because the prevailing winds on this map blow in that direction. Of course mountains can break up these flows, but if there's no terrain features it tends to create these sorts of long straight forests. This works okay on a regional map, but as the maps get bigger it starts to look very strange. So I want to implement some additional complexity in the wind model to address this.
Global wind patterns are complex, but one major component are the circulation cells that drive the trade winds. I have no intention of trying to make a realistic model of these circulation cells, but I think I can implement a simple model that captures some of the dynamics.
(Note: For simplicity's sake, I'm going to focus on an Earth-like model and primarily the northern hemisphere. There's certainly some interesting ideas in things like a planet that turns the opposite direction, or is much bigger than the Earth, etc., but those topics will have to wait on some mythical future day to be explored.)
(Warning: If you're any kind of an atmospheric scientist, please read no further. You're likely to be offended or made seriously ill by the misconceptions and bad science that will follow. Spare yourself and exit now.)
This image gives a notion of what I'm trying to implement:
The northern hemisphere has two circulation cells. Between 60 N and 30 N, the winds flow northward and turn eastward to create the westerlies. Between 30 N and the equator, the winds flow south and turn westward to create the northeast trade winds.
Dragons Abound simulates wind with a flow model. The wind in a location is represented a vector of the wind force and direction. At every time step of the model, the wind in every location is propagated forward based upon its direction. If the new location for the wind is higher, then some of the wind is turned aside while some of the wind continues upward but at less force. How the wind splits depends upon the steepness and direction of the slope. Conversely, wind going downward increases in force and turns towards the downward slope. All the wind entering a location is then summed to get the new wind force and direction for that location. This repeats until all the wind has propagated across the map and disappears out the edges. To model the circulation cells, I will need to tie the natural wind direction in a location to its latitude.
At the moment Dragons Abound doesn't know anything about the latitudes of a map, so I'm going to begin by assigning latitudes to the maps. How many degrees of latitude should a regional map like the one above cover? A degree of latitude is roughly 69 miles. I've never specified a scale for my regional maps, but it seems doubtful that they're more than 500 miles top to bottom, which would mean each map covers maybe 5-6 degrees of latitude.
The wind in a location will depend upon its latitude. From 30 degrees North to the equator is the Hadley cell. In this area, the prevailing winds blow south and turn to the west. From 30 degrees North to 60 degrees North is the Ferrel cell, where the prevailing winds blow north turning east. (Where they meet at 30 degrees North the surface wind is coming down from the upper atmosphere and then flowing off to the north or south.) The southern hemisphere is the just the reverse.
On a regional map this variation of wind direction doesn't have much effect. It's more noticeable on a continent map, particularly one that crosses over the 30 degree North latitude. Here's a composite of the top and bottom of a long continent that crosses the equator:
You can see that in northern (top) part of the map, the trade winds blow to the southwest, while in the southern (bottom) part of the map, the trade winds blow to the northwest.
Here's a map that's 4x the size of a regional map to show these wind patterns on a continent-sized map:
You can see how the wind shifts from the bottom of the map to the top, but the result is still the unrealistic-looking stripes of forest across the map.
Fundamentally, the wind model I'm using is just too simplistic to generate convincing continent-sized wind patterns. It works pretty well at capturing the impact of terrain on wind, and may even be good at capturing year-long dominant wind patterns. But biomes are shaped by not only the prevailing winds, but winds from storms, coast effects, and so on.
Of course modeling all of that would be difficult, hard to get right, and probably very slow. So I looked for a simpler alternative that might give acceptable results. One possibility that occurred to me was to run a second precipitation cycle on the map, using another wind direction. The resulting biomes would then come from a mix of the two precipitation cycles, adding complexity and (hopefully) eliminating the obvious wind alleys of the maps above.
You might think that a drawback of this approach is that doubling the precipitation would create lots of swamps and other wet biomes. Of course I could halve the precipitation in each cycle, but in fact I don't need to do that. I decide in a separate step whether a map is going to be “wet," “normal," or “dry" and then I scale the output of the precipitation model accordingly. This has a couple of advantages. First, I can select what sort of map I want without having to worry about what sort of map the precipitation model might produce on it's own. Second, it means I don't have to try to tune the precipitation model to produce a reasonable amount of precipitation across the many different sorts of maps I produce. And in this case, it means I can run the precipitation model multiple times and the normalization will adjust the precipitation to fit the kind of world I've chosen.
For the second run of the precipitation model I adjust the wind to come from 90+ degrees away from the original wind, and I also adjust the wind force to be randomly a fraction of the original wind force. Here's an example of the result:
Not a particularly interesting map, but you can see how the second wind precipitation has added complexity to the biomes. Varying the strength and direction of the second wind can make the biomes more or less different. Turning down the strength can produce something like this:
where the original wind pattern is still largely evident.
Here's an example on a more interestingly-shaped map:
Remember that I'm not particularly trying to create a procedural world model (like Dwarf Fortress, say) or even to create “realistic" biomes. I'm trying to create interesting and plausible maps. For that purpose, this approach works pretty well. The forests are sensible and indicate some underlying climate (the eastern part of the above continent clearly gets more rain than the western part), and they're also spread out and have varying sizes, which is good for the storytelling aspects of the map. So this will do for now.
The wind in a location will depend upon its latitude. From 30 degrees North to the equator is the Hadley cell. In this area, the prevailing winds blow south and turn to the west. From 30 degrees North to 60 degrees North is the Ferrel cell, where the prevailing winds blow north turning east. (Where they meet at 30 degrees North the surface wind is coming down from the upper atmosphere and then flowing off to the north or south.) The southern hemisphere is the just the reverse.
On a regional map this variation of wind direction doesn't have much effect. It's more noticeable on a continent map, particularly one that crosses over the 30 degree North latitude. Here's a composite of the top and bottom of a long continent that crosses the equator:
You can see that in northern (top) part of the map, the trade winds blow to the southwest, while in the southern (bottom) part of the map, the trade winds blow to the northwest.
Here's a map that's 4x the size of a regional map to show these wind patterns on a continent-sized map:
You can see how the wind shifts from the bottom of the map to the top, but the result is still the unrealistic-looking stripes of forest across the map.
Fundamentally, the wind model I'm using is just too simplistic to generate convincing continent-sized wind patterns. It works pretty well at capturing the impact of terrain on wind, and may even be good at capturing year-long dominant wind patterns. But biomes are shaped by not only the prevailing winds, but winds from storms, coast effects, and so on.
Of course modeling all of that would be difficult, hard to get right, and probably very slow. So I looked for a simpler alternative that might give acceptable results. One possibility that occurred to me was to run a second precipitation cycle on the map, using another wind direction. The resulting biomes would then come from a mix of the two precipitation cycles, adding complexity and (hopefully) eliminating the obvious wind alleys of the maps above.
You might think that a drawback of this approach is that doubling the precipitation would create lots of swamps and other wet biomes. Of course I could halve the precipitation in each cycle, but in fact I don't need to do that. I decide in a separate step whether a map is going to be “wet," “normal," or “dry" and then I scale the output of the precipitation model accordingly. This has a couple of advantages. First, I can select what sort of map I want without having to worry about what sort of map the precipitation model might produce on it's own. Second, it means I don't have to try to tune the precipitation model to produce a reasonable amount of precipitation across the many different sorts of maps I produce. And in this case, it means I can run the precipitation model multiple times and the normalization will adjust the precipitation to fit the kind of world I've chosen.
For the second run of the precipitation model I adjust the wind to come from 90+ degrees away from the original wind, and I also adjust the wind force to be randomly a fraction of the original wind force. Here's an example of the result:
Not a particularly interesting map, but you can see how the second wind precipitation has added complexity to the biomes. Varying the strength and direction of the second wind can make the biomes more or less different. Turning down the strength can produce something like this:
where the original wind pattern is still largely evident.
Here's an example on a more interestingly-shaped map:
Remember that I'm not particularly trying to create a procedural world model (like Dwarf Fortress, say) or even to create “realistic" biomes. I'm trying to create interesting and plausible maps. For that purpose, this approach works pretty well. The forests are sensible and indicate some underlying climate (the eastern part of the above continent clearly gets more rain than the western part), and they're also spread out and have varying sizes, which is good for the storytelling aspects of the map. So this will do for now.















































