- Going outside the map area.
- Distance of the label from its anchor point.
- Overlap between labels.
- Overlap between labels and map features.
- Label placement penalty.
So far, I've treated region labels as point labels. I calculate the centroid of a region, and I make that the anchor point for the region label. In the map below, I've marked these anchor points in red:
You can see that this doesn't always work out very well. The anchor points for Tigpolbo and Hestigbo both end up in rather awkward places. The Tigpolbo label ends up crammed into a busy area just to be close to the anchor point.
The problem is that these are area labels, so tying them to an artificial point doesn't always work well. When I was using a force layout algorithm, I addressed this by spending a lot of effort trying to find a good anchor point within the region. With simulated annealing, it makes more sense to drop the notion of an anchor point for these sorts of labels and instead just try to keep them within the area they are labeling:
- Going outside the map area.
Distance of the label from its anchor point.- Going outside the label area.
- Overlap between labels.
- Overlap between labels and map features.
- Label placement penalty.
Ideally, I don't want any part of an area label to go outside of the area, but that's fairly hard to compute (especially if the label is curved). But as a simple approximation, I can try penalizing an area label if the center of the label is outside of the area. Using this factor, the above map now looks like this:
You can see that the Tigpolbo label has moved to a much better location.
This simple approach works pretty well for regional labels because it turns out that if the center of a label is in the areas, but some other part of the label goes outside the area, the label incurs a different penalty for crossing a coast or a border. This seems to be enough to keep labels from being half-in and half-out on most maps.
It's also worthwhile to consider new ways to pick candidate locations for area labels. For point labels, new candidate locations are generated by displacing the current location, or rotating the current location around the anchor point. This makes sense because the point label wants to be near the anchor point. Random displacement works for area labels (that's what was used in the maps above) but -- since there's no need to stay near an anchor point -- it might also make sense to have also have the ability to try random points within the label's area.
To test this out, I set up area labels so that when the temperature is high, it tries random locations within the area. As the temperature gets lower, it switches over to small displacements. The idea here is to try a bunch of random locations within the area while the temperature is high and settle on the best candidate, and then to tweak that candidate around in small ways to look for minor improvements as the temperature cools off.
One challenge with doing this is finding uniform random locations within an area. That's not a straightforward problem. There are basically two solutions. The most rigorously correct solution is to divide the area (polygon) up into triangles, and then select a random triangle (based upon the area of the triangles) and then find a random point in the triangle (a known solution exists for this problem). That sounds like a lot of work. The less elegant solution is to find the bounding box for the polygon, generate a random location within the bounding box, and then test to see if that's also within the polygon. The disadvantage of this solution is that it may take multiple tries (and consequently more computing time) to hit on a point that's within the polygon, particularly if the polygon has a bad shape so that it's only a small percentage of its bounding box. However, this version is at least very easy to program.
The regions in Dragons Abound tend to be compact, which means that they'll generally work pretty well with the bounding box algorithm. Here's an example of a region, it's bounding box and candidate random locations (green inside the region and red outside):
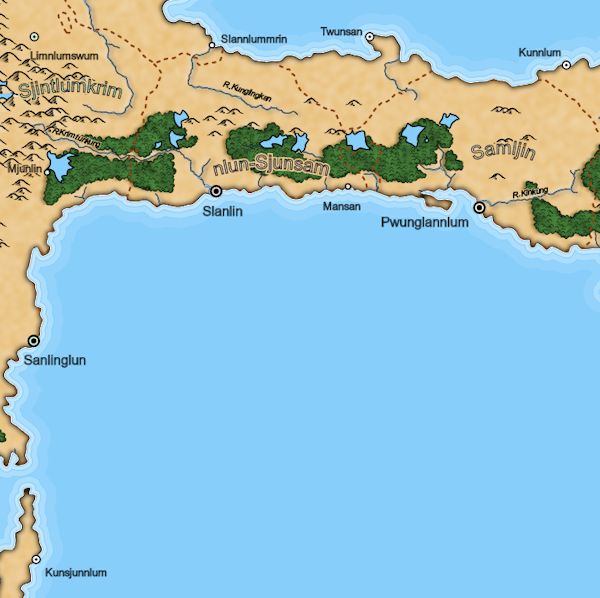
So that looks like it will work well enough for my purposes. Here's the complete area labels implementation placing the region labels on a rather challenging map where the regions are small, strangely shaped and crowded. (The random points illustration above is the "Sjintlumkrim" country on the map below.)
As you can see it does a pretty good job of finding reasonable placements even in some fairly difficult situations.
(Addendum: /u/redblobgames recently pointed me towards a small Javascript library from MapBox for finding the visual center of a polygon. This is intended to be a good position for an area label, so I modified Dragons Abound to use this as the starting point for area labels. In many cases this doesn't make much difference -- simulated annealing tends to settle on the same-ish solution regardless of the starting point -- but for some regions it's helpful to start in a good position.)