A (Not So) Minor Rewrite

I've written recently about shortcomings in my map generation caused by using Voronoi cells/Delauney triangles to define land masses.  One problem I noted when implementing barrier islands -- because land must be at least one Delauney triangle in size, barrier islands could only be made so thin.  And even with a high density of triangles, the resulting islands would be very jagged because the coastline followed the triangle edges:

Another problem was that I couldn't generate a coastline with the kind of fractal detail that you often see in maps drawn by people.  And if I did add a lot of jagged detail to the coastline, it no longer followed the land exactly, resulting in the land or the sea showing through where it shouldn't:

Here you can see spots where the land sticks out a bit past the border.

The solution to this problem is to define land (at least when drawing the map) by the space enclosed by the coastline.  This is a pretty significant change -- I rely quite heavily on the underlying grid of Delauney triangles to draw the map.  For example, I consult locations to determine the biomes, colors, and other features that should be displayed there on the map.  But using actual polygons to define land masses (even if I continue to use the underlying grid for other purposes) would bring significant benefits, so I decided to at least explore the feasibility.

(Much of the initial work for this I did on an Amtrak train ride to New Jersey, and I wasn't able to capture screenshots, so this first part will be somewhat dry.)

To begin with, I kept world generation unchanged, but as a final step I captured all the coastlines as polygons and saved them.  Initially, some of these coastlines did not form closed loops since I have avoided creating coastlines around the very edge of the map.  In the past, coastlines at the very edge of the map caused some difficulties, so I simply did not generate coastlines in those areas.  However, my work setting DA up to generate continent-sized maps removed those issues, so I was now able to modify the generation of coastlines to only create closed loops.  So now the map generates all land masses as closed-loop polygons without any holes.

Here's an example of my current approach.  The coastline follows the edges of the triangles, so each triangle falls either completely in the land or completely in the sea.  A red dot marks the center of every location that has a height greater than zero, and blue dots mark locations less than zero:

Since the coastline runs along the edges between greater than zero and less than zero, every red dot is inside the land polygon and every blue dot is outside.

When I perturb the coastline it no longer runs on the edges of the triangles.  This may result in a red dot being outside the coastline, or a blue dot inside the coastline:

Many parts of DA rely on knowing where the land and sea are, and they start to break down when the coast doesn't correspond to that split:

Here you can see how the river ends awkwardly on a non-existent coastline.

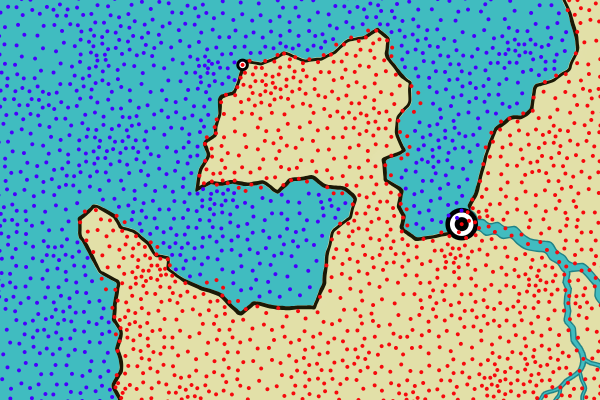
To rectify this, I want to switch over to identifying a location as “land" if it falls inside one of the land polygons.  Since the coast no longer necessarily follows the edges of the Delauney triangle, a triangle might only be partially in the land.  Rather than rely on the height in a location to decide if it is “land" or “sea" I'm now going to determine that by checking whether any part of a triangle is inside any land polygon.  In combination with this, I will mask all the land to the actual land polygons.  So even though I will paint some land locations that are outside of the actual land mass, they'll be clipped and won't show.  The trick is to include every location that has any part inside the polygon so that I get complete coverage inside.  In the following illustration, every red dot indicates a location that is at least partially within the land polygon, and every blue dot a location that is entirely outside the polygon:

Here you can see how the centers of some land locations are actually outside of the land polygon.  But crucially, none of the sea locations are inside the polygon.

However, this doesn't fix the river problem in all cases.  The river needs to be drawn past the edge of the land, so that it is clipped to the land polygon and the mouth of the river aligns with the coast.  To force the river to be drawn past the coast, I identify all the sea locations that are immediate neighbors to land locations -- I call these “coastal" locations -- and then I make sure the river extends out to a coastal region.  The result is that the river crosses the coastline and is clipped properly.  In this illustration, I've marked the coastal locations with green:

You can see the river is now clipped correctly.

With that in place, I can now experiment with making the coastline more interesting.  Here's how the coastline changes if I add a sizable amount of jitter:

This doesn't do much beyond change the shape of the coastline a little.  That's because I'm using the same line segments and just moving the endpoints around a bit.  That doesn't add any detail.  If I break the original line segments up into pieces and jitter the pieces:

The jitter adds some complexity to the coastline and oddly enough also softens it.  This is because breaking the line segments down into smaller pieces and jittering the pieces effectively creates curves.  This is a somewhat more interesting coastline, but doesn't produce the kind of fractal look I'm seeking.

Jitter moves each point randomly and independently.  It might be better to use noise to move the points around, so that nearby points move roughly together.  Octaves of noise might also help create fractal detail, as it does when creating a fractal landscape.

This certainly has a greater level of detail, but it reminds me more of a Dr. Seuss illustration than a real coastline.  There are also numerous artifacts where perturbing the coast has caused it to cross itself.

If I want a fractal coastline, perhaps I should try using a fractal generator.  There are a few articles on using fractals to generate coastlines, but nothing I can really use out of the box, so I'll have to implement it myself.

One of the simplest fractals is the Koch curve, which you've probably seen before.  The basic idea is to divide a line segment into three parts and then add a triangle to the center part.  Doing this repeatedly creates an increasingly complex shape:

Of course, this produces a perfectly regular structure, which is not what I want for a coastline, but that can probably be fixed.  So let me implement a Koch curve and apply it to a simple line segment like a bit of flat coastline:

Let's see how this looks if I vary how the line segment is split into three pieces, so that the pieces can be different sizes:

Varying the height of the bumps changes the character of the line.  With low values, the triangle becomes lower and more smooth:

Which starts to look like a coastline.  With high values a problem becomes apparent:

The line starts to overlap on itself and self-intersect.  It makes an interesting pattern but would be a problem in a coastline.

Using a negative value for the height inverts the line:

Which viewed this way looks like the silhouette of a cartoon cloud.

For my purposes, one of the most useful settings is to mix negative and positive height values, so that the fractal sometimes goes one direction and sometimes the other:

And with a lower height value:

Even this relatively unsophisticated approach looks pretty good.

Before going on, let me fix the problems that arise when the coastline self-intersects.  Trying to prevent this from happening is pretty difficult, but fixing it afterwards is straightforward.  Beginning at one end of the line, I scan ahead a segment at a time.  If the current segment intersects with a later segment in the line, I keep the intersection point and clip out everything else.

Even large height values are now okay:

Although you can see there are many spots where the line comes very close to touching itself.

At the high values, the triangle nature of the fractal is fairly evident but that can be eliminated by going deeper into the fractal (and using a thinner line to show the detail):

Before I go any further, let me try this on the coastline and see how it looks:

Well, that's disappointing.  Why did that happen?  The problem is that I'm fractalizing each segment of the coast line.  But those segments are not very long -- basically just long enough to get one triangle stuck into them -- which turns the coastline into a series of spikes/anti-spikes.  As a quick first attempt to improve this, I can use line simplification to create longer line segments on the coast:

Still rough and not quite where I want it to be, but showing enough promise to continue experimenting.

To return to the original problem of fractalizing a line, so far I've been using the Koch curve, where a part of the line is recursively replaced with a triangle (or 2/3 of a triangle).  I can change that to be a three-sided figure pretty easily:

Not unsurprisingly, this gives a more rounded fractal.  It doesn't look too bad on the map:

Increasing the number of sides quickly breaks down, because the resulting segments are too small for the next level of recursion.  The Koch triangle produces four segments of length/4.  The three-sided figure produces five segments of length/5, and so on.  With higher numbers of sides the segments quickly too small to be fractalized themselves.

Choosing a random number of sides from 2 to 4 so that each fractal varies makes the character of the curve less predictable:

So far, every recursive level of fractalization uses the same ratios of sizes.  To change that, I can borrow the notion of persistence from noise generation. With persistence, as the scale of the noise grows finer and finer, the amplitude of the noise is reduced.  If I apply that same idea here, I get a fractal line that gets smoother as the scale gets smaller:

If you compare this line to the previous one, you can see that there is similar large scale changes, but at the finer scale the line is smoother.

I can also reverse the persistence, so that at a large scale the line doesn't change as much, but there is added detail at a lower level:

Here the line is closer to the original straight line, but with strong fine detail.  This seems like it might be useful for coastlines, so that the fractalization doesn't wander too far from the original line, but still adds detail.

A limiting factor in my implementation so far is that the fractalization part only works on line segments, so when I apply it to the coastline I have to essentially throw out the existing detail and just treat that section of coastline as a straight line.  If I set the fractalization low, it's obvious that the coastline is being reduced to low resolution segments:

I call this the Picasso map.

So how can I avoid turning everything into straight lines?  In the Koch curve, the fractalization is caused by adding (two sides of) a triangle to a straight line.  I need a way to add a triangle to an arbitrary polyline.

You can think of adding the triangle to the straight line as offsetting a point in the middle of the line perpendicular to the line:

So if I want to do this to an arbitrary polyline, I need to offset perpendicular to the polyline.  In the case of a polyline, I don't have just a single line for the whole offset area, so I need to be able to offset by the perpendicular all along the polyline -- the perpendicular will keep changing.  I also need to know how far to offset along the perpendicular at any point:

So this triangle offset can be looked at as a pattern of offsets to the perpendicular by different amounts.  I'll turn the triangle offset into a pattern for the fractalization that tells me how far to offset given how far along the line I'm at -- then when I want to offset a point that is (say) 37% along the length of an arbitrary polyline I can look at a point that is 37% along the length of my fractalization pattern, find the Y value at that point, and then use that to control how far I offset the point in my polyline.

So what does it look like to apply this to a polyline rather than a line segment?  Here's a curved polyline:

And here's the same polyline after adding a triangle to it:

As you might expect, it is taller and more pointed.  That's perhaps not too interesting, but here's what it looks like if the fractalization is recursively applied (and allowed to randomly switch between negative and positive):

Since I didn't have to turn the line into a straight line, it has retained much of it's original shape.  So now I can apply fractalization to an arbitrary polyline.  Here's an example of this applied to a coastline:

The red line shows the original coastline before fractalization was applied.  You can see that unlike the Picasso Map, the original coastline did not need to be reduced to long straight lines before fractalization.   You can also see that the fractalization has made significant changes in the coastline -- eliminating big sections of land in some areas and adding some in other areas.

Now that fractalization of arbitrary coastlines is working, I want to add the capability to vary the roughness of the fractalization across the map, so that I can have smooth coastlines in some places and rough coastlines in other places.  This is evident in many real world places.  A good example is Ireland, which has a rough Western coast and a smooth Eastern coast:
Ireland's Western coast is probably rougher because it faces into the North Atlantic.  I could link this effect to ocean currents or something similar on my maps, but for a first approximation I'll just use a noise function to smoothly control the roughness of the coastline.  This view shows the original coastline in red and then the “fractalized" coastline in black underneath:

In this example, you can see that the fractalized shore follows the original coastline closely around 9 o'clock on the island, but up around 1 o'clock the shore is much rougher and deviates from the original shore quite a bit. Here's what the fractalized coasts look like on a map:

This isn't quite the look I'm aiming for, so I'm probably going to revisit this with a different approach, but it's not entirely bad.  I like very much that the coast is smooth in some places and rough in others; that's a feature I will try to maintain.